PHY 053-01
Course Syllabus Spring 2013
MWF 11:00 am - 12:15 pm 120 Olson Hall Dr. Joseph F. Alward
Office Telephone: (209) 946-3129
Office Hours:
MWF 7:15-7:45
MWF: 9:15-10:45
MWF: 12:15-1:45
Email Address: JFAlward@aol.com
Textbooks:
"Fundamentals of Physics," by Halliday, Resnick, Walker, 9th Edition.
"Physics for Engineering and Science," by Michael Browne. Publisher: Schaum's Outline Series.
There is a great deal more information on the pages of the Resnick-Halliday chapters than you are required to know. The Schaum's text better represents the content you need to understand, while the Resnick-Halliday text will provide deeper insight into the concepts than does the Schaum's text.
Study only the content in the Halliday-Resnick chapters that relate to lecture material. Attempt to work only those problems are odd-numbered (for which the answers are provided at the end of the textbook).
A recommended on-line resource is HyperPhysics, an educational website covering physics topics, hosted by Georgia State University.
This course covers mechanics, which includes vectors, linear motion, force, work, energy, momentum, rotational motion, elasticity, gravitation, fluids, and waves. To supplement the mechanics material presented in lecture and the textbooks, students may click the HyperPhysics "tree" below, then clicking again on a specific topic when the tree appears on the HyperPhysics website.
Not all of the topics in the tree are covered in this course.
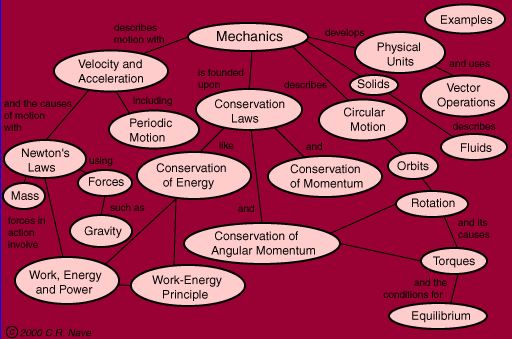
Course Schedule:
Lectures will be given on the days listed in the table below. Holidays are indicated, as well as the dates of the four examinations and final exam.
Monday |
Wednesday |
Friday |
Jan 7 |
Jan 9 |
Jan 11 |
| Jan 14 |
Jan 16 |
Jan 18 |
| Jan 21 Holiday |
Jan 23 |
Jan 25 |
| Jan 28 |
Jan 30 Exam 1 (See details below) |
Feb 1 |
| Feb 4 |
Feb 6 |
Feb 8 |
| Feb 11 |
Feb 13 |
Feb 15 |
| Feb 18 Holiday |
Feb 20 |
Feb 22 |
| Feb 25 |
Feb 27 Exam 2 (See details below) |
Mar 1 |
| Mar 4 Holiday |
Mar 6 Holiday |
Mar 8 Holiday |
| Mar 11 |
Mar 13 |
Mar 15 |
| Mar 18 |
Mar 20
|
Mar 22 |
| Mar 25 |
Mar 27 Exam 3 (See details below) |
Mar 29 Holiday |
| Apr 1 |
Apr 3 |
Apr 5 |
| Apr 8 |
Apr 10 |
Apr 12 |
| Apr 15 |
Apr 17 |
Apr 19 |
| Apr 22 Exam 4 (See details below) |
Apr 24 Classes End |
|
| Apr 29 Final Exam 8-11 am |
May 1 |
|
Final Examination
According to the schedule shown on the website at the address below, the final exam for Physics 53 will be given on Monday, April 29, 2013, from 8:00 am to 11:00 am. Students should confirm this information by clicking on the "Final Exam Schedule" link below to make sure there have been no changes.
Final Exam Schedule
Course grades will be online beginning Tuesday, May 7, 2013.
The list below of material that will be covered on the various examinations is not exhaustive. Other material, not listed below, which may have been discussed in lecture, may also appear on the examinations.
|
>>>
Examinations: (500 points) There are four 75-minute, 100-point, examinations, and one three-hour 100-point final exam. The exams covers the material described below for each exam.
Students may use one side of a sheet of 8 ½ x 11 inch paper containing any type of information to assist them during examinations.
The final examination is worth 100 points, and covers all of the material in the course. Students may use four one-sided sheets of notes to assist them during the final examination, or two sheets with notes on each side of each sheet.
Students must not have any sort of electronic communication device within reach at any time during the examinations. Sharing of calculators is also strictly forbidden, as is any other method of sharing information. Such activity will be regarded as a violation of the College's Honor Code Policy.
Exam 1: Wednesday, January 30, 2013
Material on which you may be tested includes, but is not limited to, the following:
One Dimensional Motion, Position and Displacement. Average Velocity, Average Speed. Instantaneous Velocity. Acceleration. Acceleration due to Gravity. Displacement, Velocity, and Acceleration. Integrate and Differentiate using the Calculator, and solve equations with the calculator.
Unit Vectors, Addition of Vectors, Scalar and Vector Products.
Motion in Two and Three Dimensions, Position and Displacement, Projectile Motion, Relative Motion, Circular Motion, Centripetal Acceleration, Relative Motion
Recommended reading in the Schaum's Outline text:
Chapter 1, Section 1.4 only.
Chapter 2
Chapter 3
Chapter 4
Recommended reading in the Resnick-Halliday text:
Chapter 1
Chapter 2
Chapter 3
Chapter 4
Previous Exam 1
The link above is to a page that contains Exam 1 from previous semesters. Some of the exams have solutions provided, along with corrections to typos in the solution lists. Some exams do not have solutions provided.
Exam 2: Wednesday, February 27, 2013
Material on which you may be tested includes, but is not limited to, the following:
Newton's Laws, Weight, Normal Force, Frictional Forces, Circular Motion, Centripetal Force, Tension. Kinetic Energy, Work, Work Done by Gravitational Force, Work Done by Spring Force, Work Done by Variable Forces. Power. Gravitational Potential Energy, Spring Potential Energy, Conservation of Total Mechanical Energy, Relationship between Potential Energy Function and Force. Center of Mass, Impulse, Linear Momentum, Conservation of Linear Momentum, Inelastic and Elastic Collisions, Collisions in Two Dimensions.
Recommended reading in the Schaum's text:
Chapter 5. Skip problems 37-40.
Chapter 6. Skip Supplementary Problems. There is an error on page 72 in Problem 6.1. The quantity in the parentheses should be (2π x 10.0), and the result should be 355 N.
Chapter 7. Skip Problem 7.20.
Chapter 8. Skip Section 8.4 and skip Problems 8.24-8.27.
Chapter 9. Skip Sections 9.4 and 9.5 and all problems relating to center of mass and rockets (Problems 21-26).
Recommended reading in the Resnick-Halliday text:
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Previous Exam 2
The link above is to a page that contains Exam 2 from previous semesters. Some of the exams have solutions provided, along with corrections to typos in the solution lists. Some exams do not have solutions provided.
Exam 3: March 27, 2013
Material on which you may be tested includes, but is not limited to, the following:
Rotational motion, angular displacement, velocity, acceleration, rotational kinematic equations, linear and angular variables, kinetic energy of rotation, rotational inertia, torque, Newton's Second Law for rotation, work and rotational kinetic energy. Rolling Motion, kinetic energy of rolling, angular momentum, static equilibrium. Gravitational forces, gravitational potential energy, satellite motion.
Recommended reading in the Schaum's text:
Chapter 10. Skip Problems 10.9 and 10.10. There is an error in the solution for Problem 10.18: the "1/2" that appears in the bracket should be 1/2 (M/4)(R/2)2.
Chapter 11. Skip Section 11.2 on precession, and skip Problems 9-11, 14, 15.
Chapter 12. Skip Section 12.2 on "Elasticity." Skip Problem 5, 8, 9, 16, 17, 18, 22.
Chapter 13: Skip (This chapter will be on Exam 4).
Chapter 14: Skip Problem 11, and skip the Kepler's Third Law discussion beginning near the bottom of page 162 and ending on page 163. Resume reading on page 163 with the sentence, "All of the planet orbits...."
Recommended reading in the Halliday-Resnick text:
Chapter 10
Chapter 11
Chapter 12
Chapter 13
Previous Exam 3
The link above is to a page that contains Exam 3 from previous semesters. Some of the exams have solutions provided, along with corrections to typos in the solution lists. Some exams do not have solutions provided.
Exam 4: April 22, 2013
Material on which you may be tested includes, but is not limited to, the following:
Fluids, density, pressure, fluids at rest, pressure in a fluid, Pascal's principle, Archimedes' principle, fluids in motion, Bernoulli's equation, equation of continuity. Oscillations, simple harmonic motion, equation of motion of oscillatory motion. Waves, wavelength, frequency, speed, traveling waves, waves on stretched strings, the wave equation, interference of waves, standing waves on strings, sound waves, speed of sound, traveling sound waves, interference of sound waves, intensity, decibels, beats, Doppler effect, standing sound waves in tubes.
Recommended reading in the Schaum's text:
Chapter 15. Skip Problems 11, 16, 19.
Chapter 13. Skip the discussion of "resonance" in the last paragraph on page 155. Skip Problems 20, 22, and 25.
Chapter 16. Skip Equation 16.14 and Problem 16.17.
Recommended reading in the Resnick-Halliday text:
Chapter 14
Chapter 15
Chapter 16
Chapter 17
Previous Exam 4
The link above is to a page that contains Exam 4 from previous semesters. Some of the exams have solutions provided, along with corrections to typos in the solution lists. Some exams do not have solutions provided.
Final Exam: April 29, 2013, 8:00-11:00
Previous Final Exams
The link above is to a page that contains the Final Exam from previous semesters. Some of the exams have solutions provided, along with corrections to typos in the solution lists. Some exams do not have solutions provided.
The final exam covers all of the course material.
Violations of the Honor Code
The examinations are "curved," which means that points will be added to everyone's exam depending on the class average, in order to raise the class average; some students might earn more than the 100 points "possible" on some exams. The higher the class average, the fewer will be the number of points added in the curve, and the lower will be everyone's score. It is therefore in each person's interest that the class average relative to their own score be low. Students who are perceived as taking an unfair advantage during examinations, thereby raising the class average, are usually reported to the professor by other students. It is therefore important that all students make certain not to be seen by other students using a cell phone or any other communication device during examinations, or looking at another student's answer sheet. Several times in the past, following several complaints by observant students, investigations of students' use of cell phones during exams were conducted, with the result that the offending students were reported to the Office of Judicial Affairs. Almost every semester in every class students report violations to the professor and, following Judicial Affairs Hearings,the offending student is given a zero on the exam, or worse. Do not be seen using a cell phone during exams, or be seen talking to other students, because someone is certain to report you.
Other examples of violations of the honor code include, but are not limited to, verbal communications with other students during exams, and using more than the allowed amount of notes. On each of the four examinations, students may use one side of one sheet of paper filled with any information; using more than one side of one sheet is a violation of the honor code. On the final exam, students may use four sides of four sheets of paper, or two sides of two sheets, or other combinations of sides that do not total more than four sides.
The College of the Pacific Honor Code Policy
Approved by COP Council: November, 2009
The College of the Pacific holds all of its students to a strict standard of academic integrity. In the case of a suspected violation of the University academic honor code, the faculty member and the chair of the department will evaluate the alleged infraction and report it immediately to both the chair of the department, the College Academic Affairs office, and the Office of Judicial Affairs, which will begin a formal investigation.
If the Office of Judicial Affairs determines that the student was is responsible for the honor code violation, the standard penalty in the College is failure of the assignment and/or the course. In such cases, the student will be prevented from dropping or withdrawing from the course, even if the deadline to do so has not expired. Further disciplinary action may also be taken by the Office of Judicial Affairs |
|
Grading
Laboratory: (120 points)
Students meet 12 times to work in teams to complete laboratory exercises related to the concepts discussed in the lectures. There are 10 points possible for each lab meeting. Bring a calculator to every session. No laboratory notebook or text is required; no advance work is necessary and all work completed during the lab period is turned in at the end of the period. There are no make-up labs.
Replacing the Two Lower Exam Scores
The two lower of the four exam scores will be replaced by the final examination score, provided the final exam score is higher than the lower scores; if the final exam score is not higher than the lower scores, no replacement will be made. For example, if a student received 40 and 50 on the first two exams, but got a 90 on the final exam, those two exam scores will be erased and replaced by 90. Thus, a student who had two of the four exam scores in the "failing" range can still earn an "A" in the course.
Any examination score that is voided as the result of a proved violation of the Student Honor Code will not be replaced by the final examination score.
Curving the Exams
The exams are curved, depending on the class average. Some students may receive more than 100 points on a 100-point exam because of their additional points that might have been added to everyone's score in the curving process.
Some test-taking advice
Quickly scan the exam problems, taking note of those which you think are the harder problems. Save those for last. It's very important that you not spend too much time on any one problem as this might prevent you from discovering two or three simpler problems you have not yet worked, but which can quickly be answered. Look for the easy problems, and work those first. The worst thing that can happen to test-takers is to run into a difficult problem early in the exam period, waste several minutes on it, still not get the answer, and not only lose all that time, but lose considerable confidence as well, and then rush to make up lost time and in their haste make mistakes.
There are no make-up, late, or early exams; if a student misses an exam, that exam will count as one of the students two lower scores, which might be replaced by the final exam score.
There are 500 points possible for the five exams; some students, because of curving, may actually receive more than 500 points for the five exams.
There are 120 points possible for the lab, for a total of 620 points. Your course grade will be based on following percentage scale:
92-100: A
90-92: A-
88-90: B+
82-88: B
80-82: B-
78-80: C+
72-78: C
70-72: C-
68-70: D+
60-68: D
0-60: F
In the event your course percentage falls exactly on the dividing line, such as 92.00, for example, you will be given the higher grade (in this example, A). Course percentages are not rounded, so if your course percentage, for example, is 89.9999%, your course grade will be a B+. If it is exactly 90%, your course grade is an A-.
A student whose average on the five exams is, say, 77 (a "C"), but who collects the typical number of points in the laboratory (about 115 out of 120), would have a course total of 500 points out of 620, or 80.65% (a B-). This example illustrates how important the lab score is in determining the student's final grade. Attend lab, finish it (everyone does), and you will probably earn about 115-120 points, which usually makes a huge difference in your course grade.
Frequently Asked Questions Regarding Grading
"What grade do I need on the final to get a B (for example)?"
A hypothetical student got 114 points out 120 points in the lab, and the following scores on four exams: 48 67 75 86. She or he needs 82% of 620 points, or 0.82 x 620 = 508.40. Assume that the final exam score will be higher than the "48" and "67" received on two of the exams. Let x = final exam score. The five exam scores, plus the lab score, must be at least 509:
x + x + 75 + 86 + x + 114 = 509. Solving for x, and rounding up, we get x = 78. If the student gets 78 or higher on the final exam, he or she will be guaranteed at least a B in the course.
|